Don’t Go Changin’ That Invariant

---

Where we learn that there’s a mathematical reason why your “happy place” is your happy place.

I’m going to tell you about one of those words that has a definition that can be ever-so-slightly different depending on not just the context of how it’s being used, or what part of speech is assigned to it (Sometimes it’s a noun! Sometimes it’s an adjective!) but its definition can also be different depending upon the field or even program of study the word is being used in.

This word is invariant.

---

DEFINED AS…
At its most core definition, it means never changing, like – never ever changing –  and it’s used as an adjective, as in: Even if someone cracked a joke, the invariant expression on the poker player’s face revealed no emotion whatsoever.

In the fields of math and science the word has deeper significance. Invariant not only means constant and unchanging, but it means constant and unchanging even if the conditions that it’s in changes. It doesn’t matter if a gentle breeze caresses it or a hurricane tumbles over it, neither of those things will affect a change in the designated invariant.

Identifying an invariant in the sciences, something like physics (a discipline which, you know, has some math at its very core) gives us a few more dependencies to work with.

A number that is unchanged by a transformation, (where) a transformation is
something like a rotation or moving a system from one place to another.

The Universe in the Rearview Mirror by Dave Goldberg (pg 108)

It’s at this point in my research that I realize the word ‘invariant’ is no longer classified as solely an adjective. Nope, now we’re talking about it being used as a noun.

The definition of invariant – where the word ‘transformation’ is prominent – is same-same in any branch of mathematics that’s primarily focused on spatial areas, especially when there’s a change that happens due to some sort of movement. So, the word pops-up a lot in Combinatorics (the mathematics of counting & arranging [what are usually] large quantities), in Topology (the mathematics of shapes & objects within a defined space) as well as in the familiar-to-us-all mathematics branch of Geometry (the mathematics of the relationship of shapes and their measurements and their properties and their angles and, actually, topology is a part of geometry.

So, the word ‘invariant’ – in much of math and science – is most commonly used as a noun and its definition includes the words movement or transformation.

Invariant
(noun)
In mathematics, a quantity or expression that is constant throughout a certain range of conditions.

Dictionary.com

---

EXISTING AS…
It’s probably no surprise to you that I am most inspired by the mathematical definition specifically because of the reference to transformation, to movement.

Realizing that made me feel certain that
we all have at least one invariant (noun) in our life.

I’d say that for each of our own invariants, that no matter what happens to the conditions your personal invariant exists in nor the transformations that might physically affect it, it remains, for you, never changing. It could be a house you lived in and no matter what furniture is in it, or what time of day it is, or even who lives there, it still feels the same to you. Or perhaps it is a bookstore, and no matter where the books move around in it or who owns the place, it feels the same to you as it did the first time you were ever there. It could be a specific chair. It could be that one teacher, long ago.

The Ocean (any of the five oceans, actually) is the epitome of an invariant for me, and it is definitely my favorite one. I grew up on the Atlantic and I’ve spent the last couple of decades on the Pacific, and I’ve visited other oceans, and they all do the same thing for me, to me.

It through-and-through calms me. It doesn’t matter if I am standing on a dune or at the shoreline or if I’m headed south on Hwy 101 and I get my first glimpse of the ocean as I round a bend; I see her, and my whole physical being (especially my arms?!) settle down.

I think of these spatial invariants as very sensory.

So no matter if there is new construction at my favorite beach or if the shoreline is covered in jellyfish, the ocean is My Favorite Invariant. Its conditions are constantly changing – heck, you expect them to change, it’s not a surprise when they change. But your experience of the invariant remains constant. It is still exactly as it’s always been, as far as you are concerned. Dependable. I’d even say that my invariant is my safe place.

Oh, I’ve been tested. I’ve had arguments on the beach, but I don’t avoid that beach because the ocean still gives me all the goodness it has always given me, right there, in that exact same physical spot. I have had great sadness churn up inside me because I miss my mom whenever I sit on the bench that we always sat on together, both of us staring at the ocean. Looking at that ocean from that bench still wraps me in calmness, that hasn’t changed at all. It’s just that now, since my mom died last year, that calm feeling just exists in a space that has changed and expanded to also include a bit of sorrow in it now.

Are you getting it? Are you thinking about what Your Invariant is? Since we’re using it as a noun, just as the math kids do, it follows that your invariant could be a person, place, or thing. Woah.

---

FELT AS…
Here’s my hypothesis: In this particular mathematically-based definition of what an invariant is, where the checklist of invariant identification is heavily spatially-related leading to a direct tie to a person’s sensory reactions, and now that I’ve also called out a bunch of physicality to the word, I propose that there is a direct relationship between your favorite invariant and your longest cranial nerve, the vagus nerve.

While some cranial nerves have either sensory or motor functions, others have both.

The vagus nerve is such a nerve. … and is responsible for various internal organ functions, including:
>digestion
>heart rate
>breathing
>cardiovascular activity
>reflex actions, such as coughing, sneezing, swallowing, and vomiting

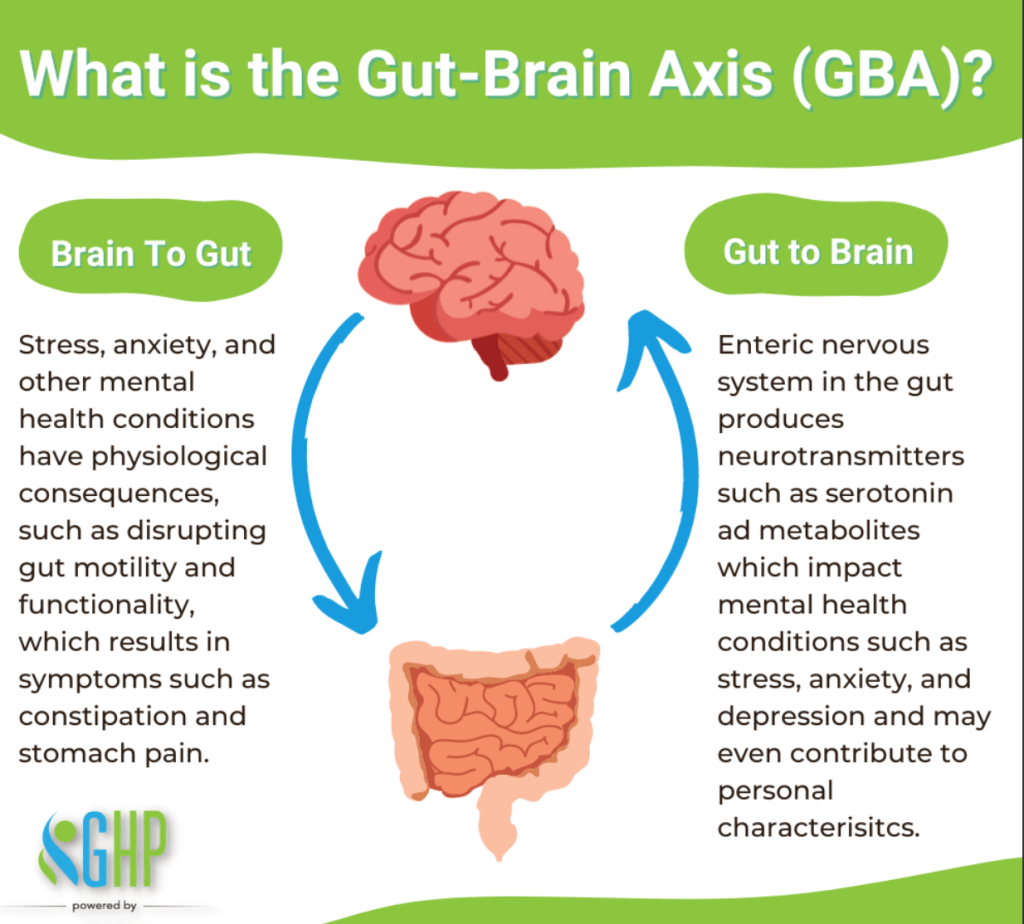
It plays a role in the autonomic nervous system, which controls actions people do unconsciously, such as breathing and digestion. It may also form a link between the gut and the brain, playing a role in what scientists call the gut-brain axis.

The vagus nerve sensory functions are divided into two components:
1. Somatic components. These are sensations felt on the skin or in the muscles.
2. Visceral components. These are sensations felt in the organs of the body

excerpted from Vagus Nerve: Function, Stimulation, and More

Gut-brain axis? Ok, so, it’s a linkage point that is activated involuntarily by you – it’s basically a meet-up point, it’s the shared conference room – where your body and brain have a lightning fast discussion and exchange an up-to-the-minute status report of what they are both observing and they quick-like make a decision that the way that you will consciously be affected by your invariant is that…you’ll get goosebumps on your arms. Or, an itchy flush of heat will rise up on your neck. Or the pit of your stomach drops. Or you feel a physical release within that deposits you into a state of calmness.

What up with that, vagus nerve? Huh, look at you and all that power you’ve got going on.

I hereby offer to the universe this definition for the word invariant as used in the program of study called IRL 😉:

Invariant
(noun)
A never changing spatial sensorial; that which elicits a familiar somatic or visceral reaction.

Kate Ertmann of Kate Loves Math*

My definition allows for the human-side of math. It meditates in physiology because it acknowledges not just the power of the vagus nerve within us all but also the fact that what may make me nervous or excited or feeling safe may not be the same thing for you – or you – or even them, over there.

But when my invariant is the same as your invariant, well, that could be a solid base for a deep connection with another person. I really do think a human connection like that offers great value to a relationship.

Like mathematicians are thankful for the dependability of things in their world of research, us everyday humans can relate because we are thankful for an invariant (as a noun) in our life .

Thanks math, you’re the best.